 Okay. I’ve figured out the answer: park factors.
Okay. I’ve figured out the answer: park factors.
The question, of course, is what vaporized so much of the variance explained by FanGraphs’s runs-produced above average statistic (wRAA) when FG converted it into the hitting element of its WAR measure.
Park factors. Pretty much all of the loss—from nearly 90% to under 70% of variance explained in team runs per game—comes from park factors. Or that’s what seems to be going on.
I had to figure this out quasi-experimentally.
It’s not feasible, really, to trace out directly the steps that lead to FanGraphs’ Offensive War R2 loss. You can observe it in the manner that I did a couple of posts ago—by directly comparing the runs-scored variance explained by FG’s wRAA and offensive WAR measures.
But to reliably reconstruct the process that leads to this outcome, I think you’d need more data than FanGraphs supplies. Where a player divides his time between two or more teams in a season, FanGraphs publishes only his overall and not his team-specific stats. That means you can’t reproduce team-level stats by aggregating those of all a team’s players. Because you can’t do that, you can’t disassemble the team-level stats by, essentially, removing from its individual player’s stats the various things FG does to translate their wRAAs into offensive WAR scores before you add them all up.
So I decided to perform that set of operations on my own OPSrp—an OPS-derived run production measure.
I’ve discussed how I created and that measure, and confirmed that when you aggregate the OPSrps of teams’ individual players season-by-season, you get a super high R2 for team runs scored comparable to the one you get when you regress team runs on FanGraph’s admirable wRAA measure.
I demonstrated, too, that when you translate OPSrp into a team-level wins above average score (OPS-WAA), you really don’t lose very much explanatory power at all.
So I figured the way to identify exactly what FanGraphs was doing that extinguished so much of the explanatory power of its individual runs-produced measure was to do to OPSrp exactly what FanGraphs does to wRAA in the course of translating it into its offensive WAR measure.
When I did, I found out that my two conjectures about where the R2 had gone were just wrong!
I had speculated that the problems might have been FG’s uniform “runs to wins” formula, which disregards the nonlinear relationship between the two. Or alterantively, its recalibration of runs/wins above average to runs/wins above replacement, which truncates the distribution of player performances.
Well, those reduced the variance explained of my own OPSrp wins above average measure (OPS-WAA) by no more than 2%. Yup—another set of conjectures bites the dust.
But when I made the park factor adjustment—BAM!—my wins above average measure R2 sunk by 15%!
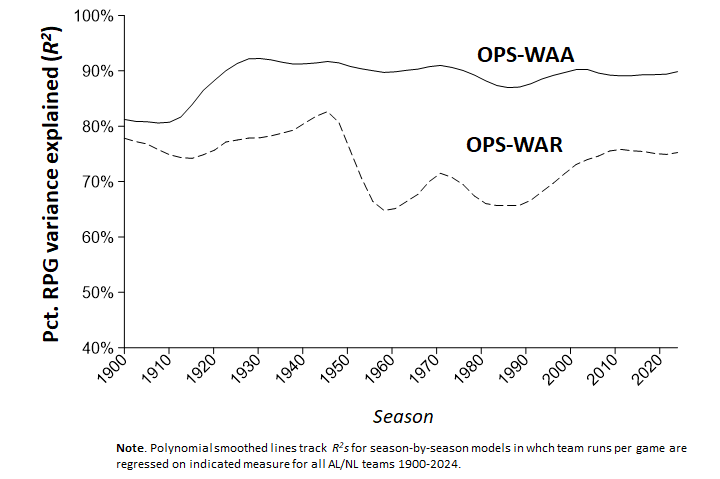
That’s not quite as big a hit as FG’s measure took. But like I said, I wasn’t able to re/deconstruct it in a manner that allowed me to see exactly where the R2 loss happened. So I’m going to assume, with a good degree of confidence, that there wasn’t anything else that resulted in lost R2 besides FG’s addition of park factors .
What to say about all this? Well, I can think of a couple of things.
First, there’s a tradeoff to be made here. As was noted in a very insightful discussion by Brandon Heipple a few years back it’s pretty obvious that park factors are going to reduce the explanatory power of any offensive production metric. The whole point of PFs is to flatten out variance by tamping down the predicted productivity of players who got the benefit of “hitter friendly” stadiums and puffing up the predicted productivity of players who were handicapped by “hitter unfriendly” ones.
If, like me, you are principally trying to model runs scored as accurately as possible, you might not like that so much.
 But as Heipple notes, there are lots of inferences people (himself included) want to make that are improved by valid PFs. By removing the impact of disparately configured parks, PFs enable a more fair comparison of “true” or “context free” individual batter proficiency. And if one is trying to make predictions about what will happen if a player is moved from one team to another—as MLB front offices have to do—then valid PFs are essential!
But as Heipple notes, there are lots of inferences people (himself included) want to make that are improved by valid PFs. By removing the impact of disparately configured parks, PFs enable a more fair comparison of “true” or “context free” individual batter proficiency. And if one is trying to make predictions about what will happen if a player is moved from one team to another—as MLB front offices have to do—then valid PFs are essential!
But second, one has be very confident that the park factor one is using are valid. PFs come at a big cost in predictive accuracy. If they don’t improve the counter-factual estimate of hitter performance they are enabling by at least that amount, then they are making one’s judgment of how hitters perform in neutral or different environments worse, not better.
A number of very good studies suggest reason to worry that this is exactly what his happening. One, published in the Journal of Quantitative Sports Analysis, showed that the normal equation for computing park factors inherently overstates the impact of so-called hitters’ parks.
In another, Bill Petti found that when players move to more hitter-friendly parks, a conventionally formulated park factor overestimated the impact on their wOBAs by a ratio of over 4:1 for players with 300 PAs, and 5:1 for those with the most power.
That degree of over overshooting will almost certainly exceed the difference in performance between a hitter’s raw runs-produced estimate and a valid park-adjusted one. And if that happens, then indeed, the PF-adjusted metric will generate a “context free” estimate of performance that is less accurate than would the unadjusted run-productivity one associated with FG’s wRAA or with my OPSrp alternative.
These sorts of results suggest the need for a more empirically grounded approach here. (BTW, if you want to do your own research here, then check out Charlie Pavitt’s invaluable compendium of sabermetrics research!)
I’m not saying I’m going to try to produce it. But if I were to continue down this path, I’d take a hard look at sophisticated methods that Michael Schell uses (and validates) in his classic historical comparison of hitters—since I’d be completely unsurprised to discover that those would do the job very nicely!
In the meantime, though, I will just keep plodding along in the project that interests me most, which is maximizing explanatory and predictive power—subject to standardization when I want to remove the vagaries of playing conditions from the equation.
