Well, with reluctance and trepidation, I’ve pretty much concluded that Stephen Jay Gould’s (r)evolutionary conjecture on the variability of sports performances is wrong.
You might know (or if you have been following my own journey learned) that Gould famously conjectured that athletic performances can be expected to become less variable as a sport matures. This dynamic reflects selection forces akin to those in evolution. Just as members of a species can be expected to converge on a fitness-promoting gene mutation, so athletes can be expected to converge on a trait that promotes successful performance, thereby reducing variability in that trait.
Gould applied that insight to batting averages and used it to explain the extinction of the .400 hitter: as baseball players become more and more proficient at hitting—and pitchers at preventing the same—there will be a contraction of variance in hitting ability, making it less and less likely that a batter will exceed the mean in hitting by enough standard deviations to bat .400. This conjecture has figured generally in sports research and in particular in the great baseball hitting-performance studies of biostatistician Michael Schell.
The primary empirical support for Gould’s conjecture was the general decline in standard deviations in major league batting averages over time.
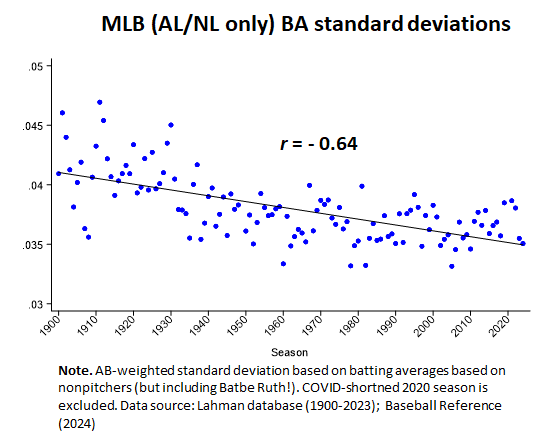I encountered a couple of divergences from this pattern recently, one for slugging pct. and the other for fielding-independent pitching (FIP):
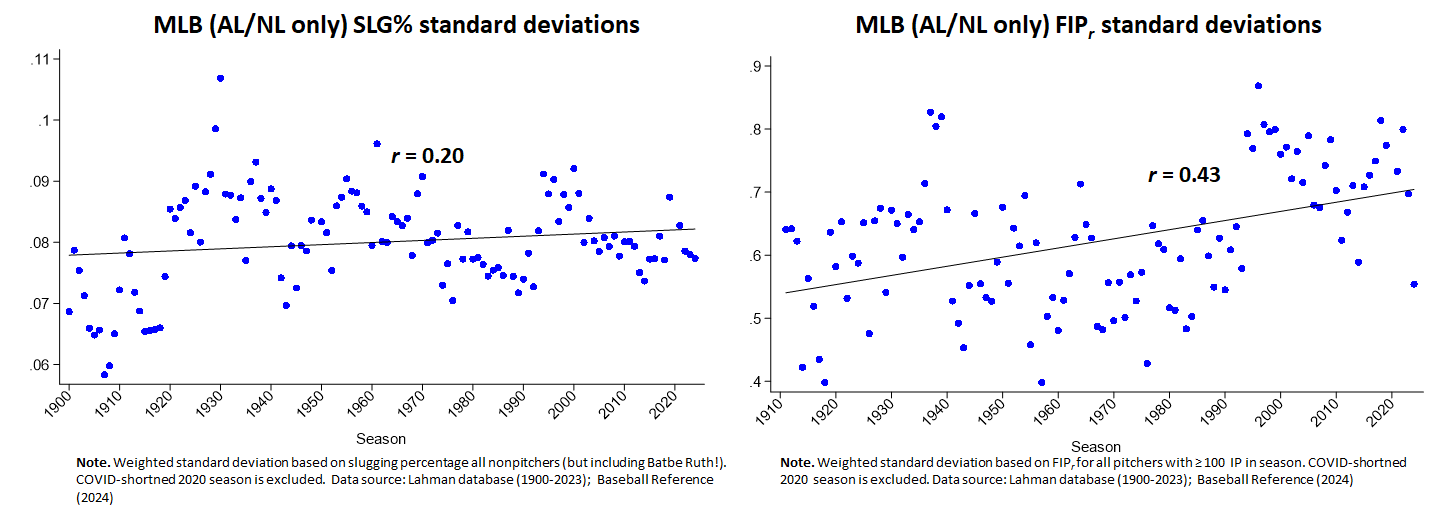
I got all excited thinking maybe this deviation indicated an evolutionary mutation in the game associated with baseball’s “Great Transformation”—the recent emergence of strikeout-vs-home run showdowns as the game’s central dynamic.
But now I doubt that’s what’s going on. To begin, I’m not really sure an uptick in SDs would be associated with “evolution” in the game. Maybe weird industry-associated constraints on selection forces could produce this but I think it is actually more likely that selection effects would generate an immediate or at least reasonably immediate reduction in variability in response to the emergence of any skill or playing style that increased outcome success—not a phase of increased variability followed by a trend toward nonvariability.
But in any case, I widened the scope of my examination of the phenomenon and discovered patterns that cannot be reconciled with Gould’s conjecture. E.g., home-run allowed rates for pitchers have become a lot more variable:
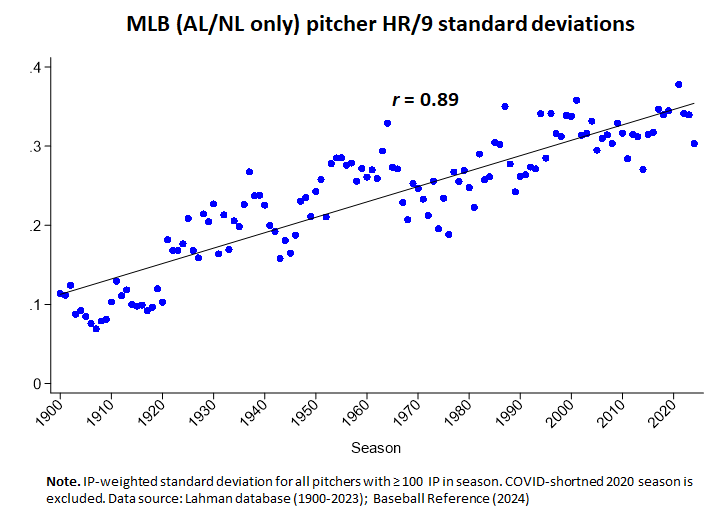
That doesn’t seem to be what Gould would predict. . . .
Or take a look at other sports. In hockey, the trend in player goals per game (for both forwards and defensemen, by the way), has fluctuated in a manner that doesn’t fit Gould’s prediction of steady decline.
Even more significantly, in football, SDs for rushing yards per game by running backs has steadily increased. Surely, that’s an area where the improving proficiency of offensive and defensive players would have predicted reduced variability under Gould’s theory.
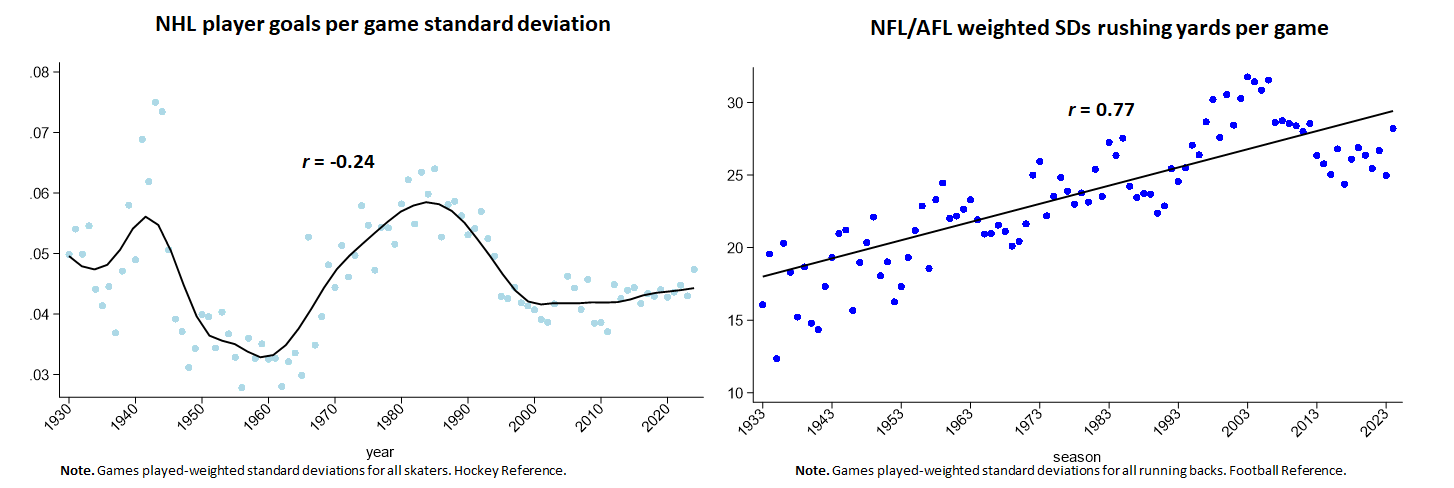
So Gould’s conjecture is either wrong or just a special case of some more global account of how variability fluctuates in sports performance in response to changing game dynamics.
Indeed, I wouldn’t just write off trends like this as meaningless. I think it probably is the case that trends in variability are responsive to something important in how different sports develop, and it would be really cool to figure out what that is!
I don’t even have a set of candidate conjectures on this—the whole topic is new to me!
But if others have ideas, I’d certainly be keen to investigate them.
