Okay, so here’s another crazy one. Look!
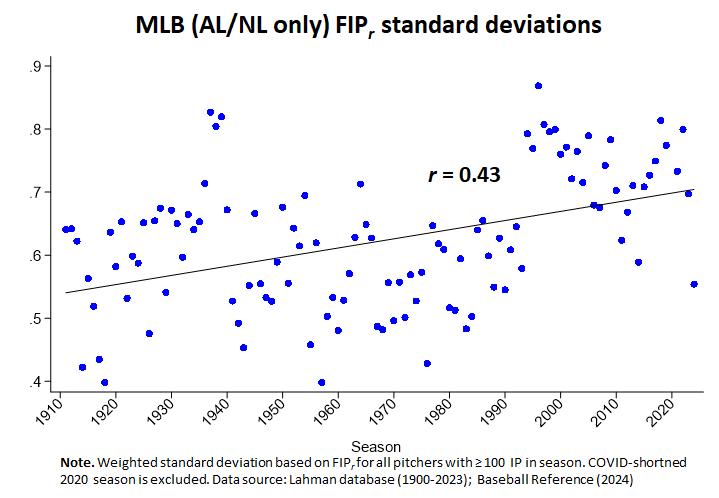
See it? It’s another Gould-defying trend in a baseball-performance standard deviations!
I suppose it makes sense to start with what it’s the standard deviation of.
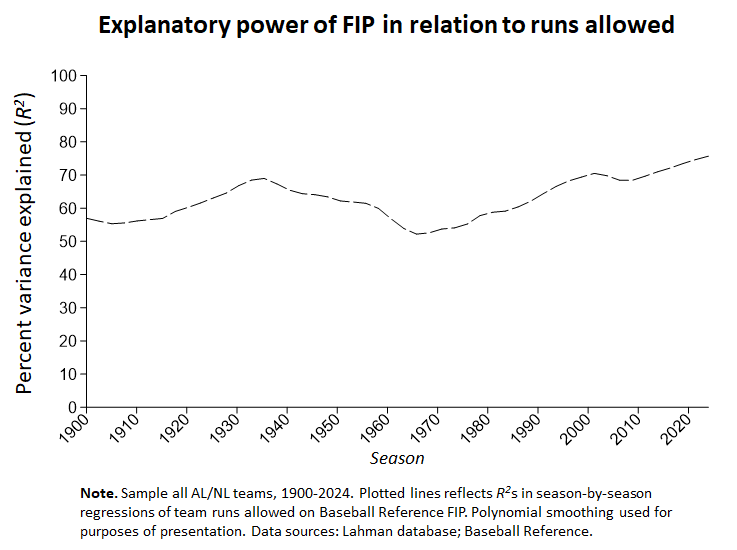
Basically, it’s a regression-derived fielding-independent pitching (FIP) metric. FIP is an index comprising a pitcher’s strike out rate, home-run allowed rate, and hit-by-pitch rate. These are all elements of run-avoidance that don’t depend on the quality of the defense that backs the pitcher up.
To calculate a metric of this sort, I regressed runs allowed per game for every pitcher for every season (≥ 100 IP) of AL and NL history against his (season-specific) strikeouts per 9/IP, HR/IP & HBP/IP. The resulting equation generates an expected run-per-game number—call it FIPr –that can be assigned to each of those pitchers based on his strikeout rate, home-run allowed rate, and hit-batter rate. (I’m calling it FIPr because it uses regression weights rather than fixed theory-derived weights for the elements of FIP, but that’s not a big deal here and I’ll talk more about that some other time).
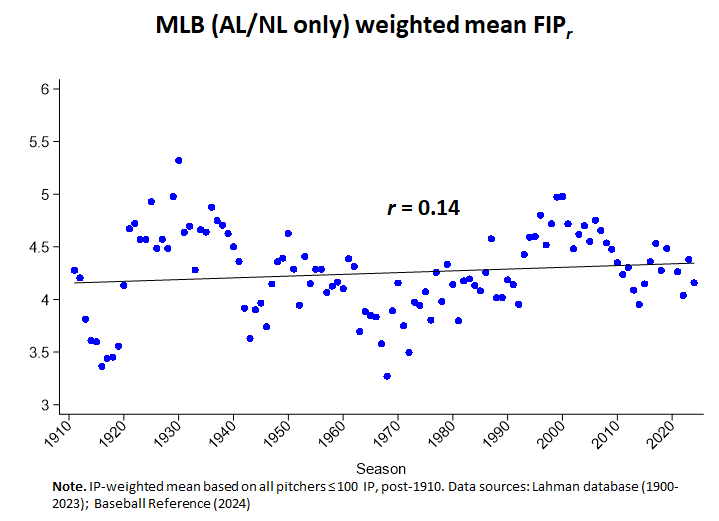
That number is perfectly sensible. Looking at the (IP-weighted) average of FIPr across MLB history, we learn that these characteristics make the average pitcher individually “responsible” for around 4.30 runs a game—although that average has cycled up and down, just like every other performance metric, in response to transient shifts in game conditions.
But most of those metrics have over time become less variable across players.
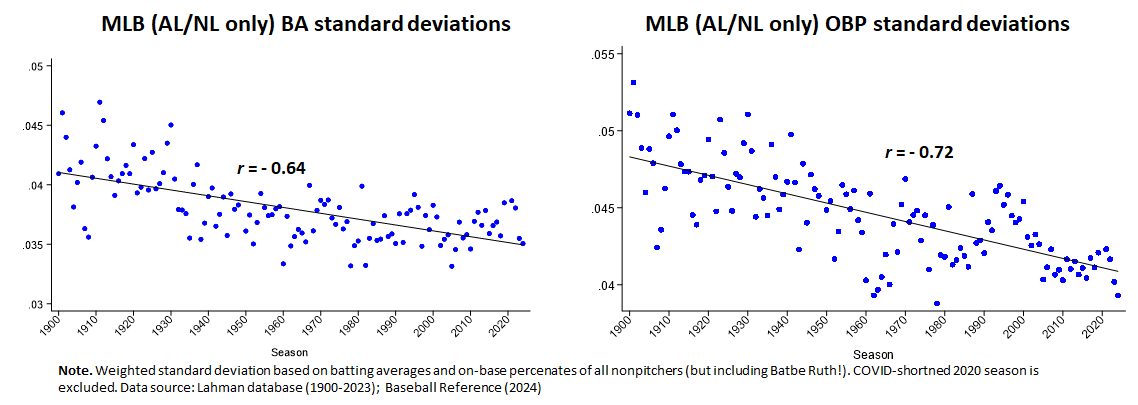
As I said a few days ago, this is a dynamic that Stephen Jay Gould analogized to the reduction in diversity observed in a species as its members converge on a fitness-producing trait. Basically, if something is good for an organism—like, say, on-base percentage, for a major league batter—than over time members of that species will be selected for that trait (and just as critically on the power to negate it). Variability, measured by SDs, will get smaller.
That’s what has happened with batting averages, e.g., and is part of the reason we shouldn’t expect to see any more .400 hitters: as hitters converge on the mean (which is declining, too, at least at the moment), it’s too hard to get enough SDs from it to hit .400.
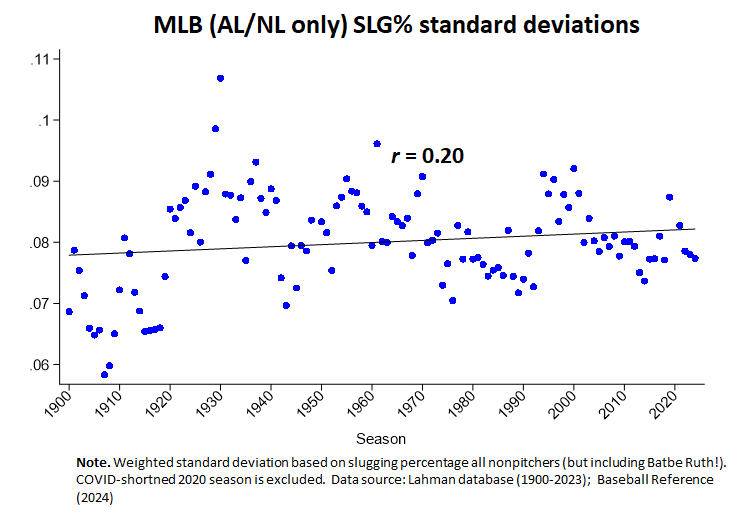
But as I showed the other day, slugging percentage seems to defy this pattern. Its SD has been rising gradually.
And now look: SDs for fielding-independent pitching (as measured by FIPr) have been increasing, too, at an even steeper rate.
What the?!…
When I saw this expectation-defying pattern in connection with SLG%, I surmised that maybe the game was evolving in some manner—viz., towards more power hitting, as reflected in the surge in HR rates in the last quarter century.
I think that is even more plausible here. FIP has always been a really important predictor of runs-avoided success. But it has really taken off in the last 3 decades. It’s increasing contribution to avoidance of runs is an incidence of the Great Transformation of the game toward strikeout-vs-home run showdowns (it also has drained differences in team fielding quality of most of their importance, something I examine in this paper).
As FIP becomes more and more critical for success, teams have aggressively begun to select on the qualities that generate it when they develop, acquire, and retain pitchers. But this fitness-promoting mutation in the game hasn’t yet fully replicated itself out across the pool of potential players (or across the various systems that operate together to populate major league pitching staffs). Until it does (it won’t take long), there will be more variability in that aspect of pitching success than there are in aspects of performance that have been of consequence for longer periods of time. . . .
I don’t know if this is true, of course. Indeed, I wish I had a good alternative hypothesis to pit against it for empirical testing.
Maybe someone can suggest one? If you want to jump start your conjecture imagination with some data, I’ve posted the ones I used here in the data library.
Anyway, it’s freaky, right? And I’m now going to look at pretty much every damn indicator of player proficiency to see if that helps me figure this out.
What else can I do?
2 Responses
Interesting… looks like season-over-season SD is relatively stable (if noisy) up until 1990s… at which point there were some important changes in the players that led to changes in the game.
The number of instances in a baseball season should reduce variance, but with home run hitting being inherently more variable, I can see how FIP’s variability would go upwards when there’s a tactical change towards HR hitting in the game. Does that make sense?
Good points.
BTW, I think I’ve given up on evolution thesis, although my views are still in flux. I say more here. I think a large issue is that it makes little sense to assume that selection forces will operate in professional sports the way they do in nature, where evolution never cuts unfit species any slack, and economic markets, where unprofitable firms can’t survive either. In sports, teams are playthings for billionaires, some of whom (like Jerry Reinsdorf, e.g.,) likely are impervious to the annihilation of their teams on the field.
But as for shifts in FIP SD:
1. I have created a polynomial rendering of the FIP SDs, which you can find in this post. For sure confirms your observation about timing.
2. The “Great Transformation”—from resourceful pitching & slick fielding against consisting hitting to today’s perpetual loop of strikeout specialists vs. homerun brutes—could I suppose affect variance in FIP.
But I don’t know, really, how to think about this. It comes down in part, again, to what we should expect to see when baseball game dynamics shift; should there be phases of change in variance and how long should they be? Or will all of that be confounded by competition-indifferent industry forces?
Also, take a look at the SDs for HR/9IP and K/9IP. They both rise consistently across the entire history of baseball, so that sort of variance can’t be a consequence of the Great Transformation.
There is a lot to learn by studying these things, I suspect.
BTW, I assume you when say Jeter was right you are referring to his prediction, made after his rookie season, the the Higgs-Boson would be discovered by 2015? I think he just got lucky there