The simulation routine used to predict Super Rookies vs. ’27 Yankees series is going to have to evolve if it has a future. But why not at least give the BBC&S-imulator 9000 a chance at some real-world predictions first?
Using the same model and Monte Carlo simulation algorithm as before, I took a shot at predicting/handicapping the LCS’s. The matchups aren’t nearly as close the Rookie-Yanks series was predicted to be.
Start with the NL. The respective WAR-per-games of the Dodgers and Mets are 0.286 and 0.219, respectively. The model rates that a 57% heads-up, single-game advantage for the Dodgers.

Naturally that translates into an even bigger edge in a seven-game series. The Dodgers won 67% of the 2,500 simulated best of 7’s. Thirty-six percent of the series ended in either 4-1 or 4-2 victories for LA.

That’s a more decided advantage than is now being placed on the series by sports books, which as of this writing rate the Dodgers as about a 3-2 favorite after removing the hold. Still, when the skew built into the betting lines is taken into account, you’d have to win about 64% of the time to break even on a Dodgers wager (-176) and 40% of the time to break even on a Mets-to-win bet (+148).
I’ll pass!
The respective WAR-per-games of the Yankees and Guardians are .293 and .228, respectively. That again translates into a 57% one-game edge, this time for the Yankees. And again, a 66%-33% advantage for the series, as determined via a 2,500 game simulation.
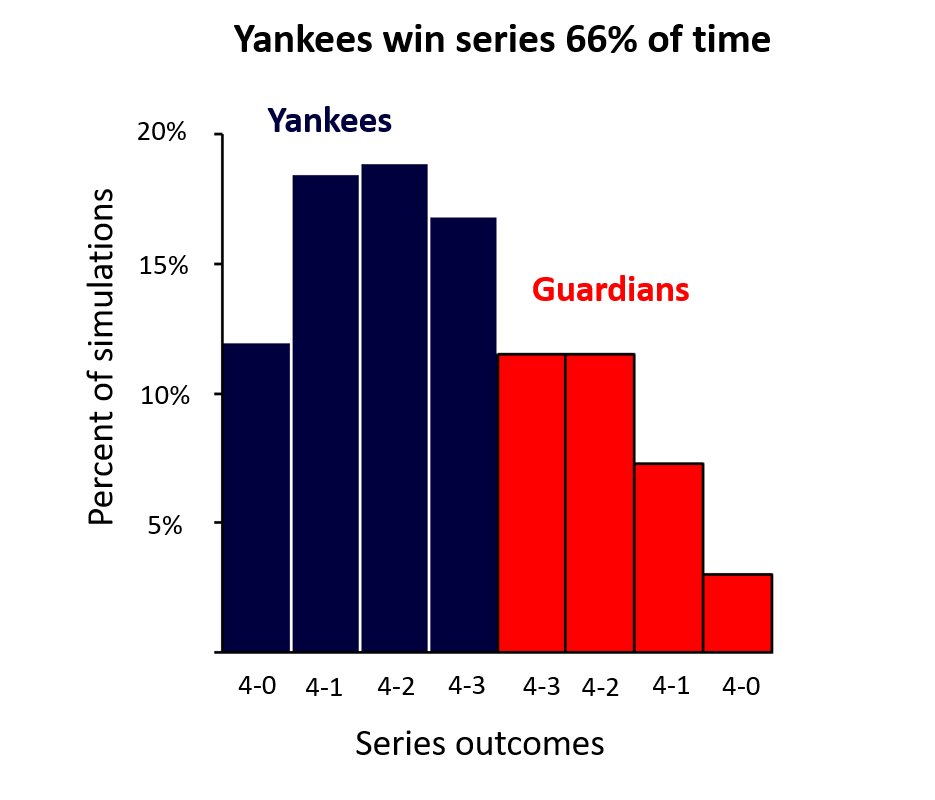
Any betting value here? The effective odds at books favor Yankees slightly better than 3-2 (63%). But at -190, you’d have to win 66% of the time. At +160, a Guardians bet would have to win 38.5%. Pass!

I’ve uploaded the simulation script to the same page that contains the materials necessary to replicate the Super Rookies/’27 Yankees series. This script makes it easier to plug in numbers for any 7-game series you care to simulate. All you have to figure out on your own is the WAR-per-game totals for the teams.
Let’s see what happens, and give it another go for World Series.
