I’m going to show you something weird that I spotted recently. Ready? Here it is:
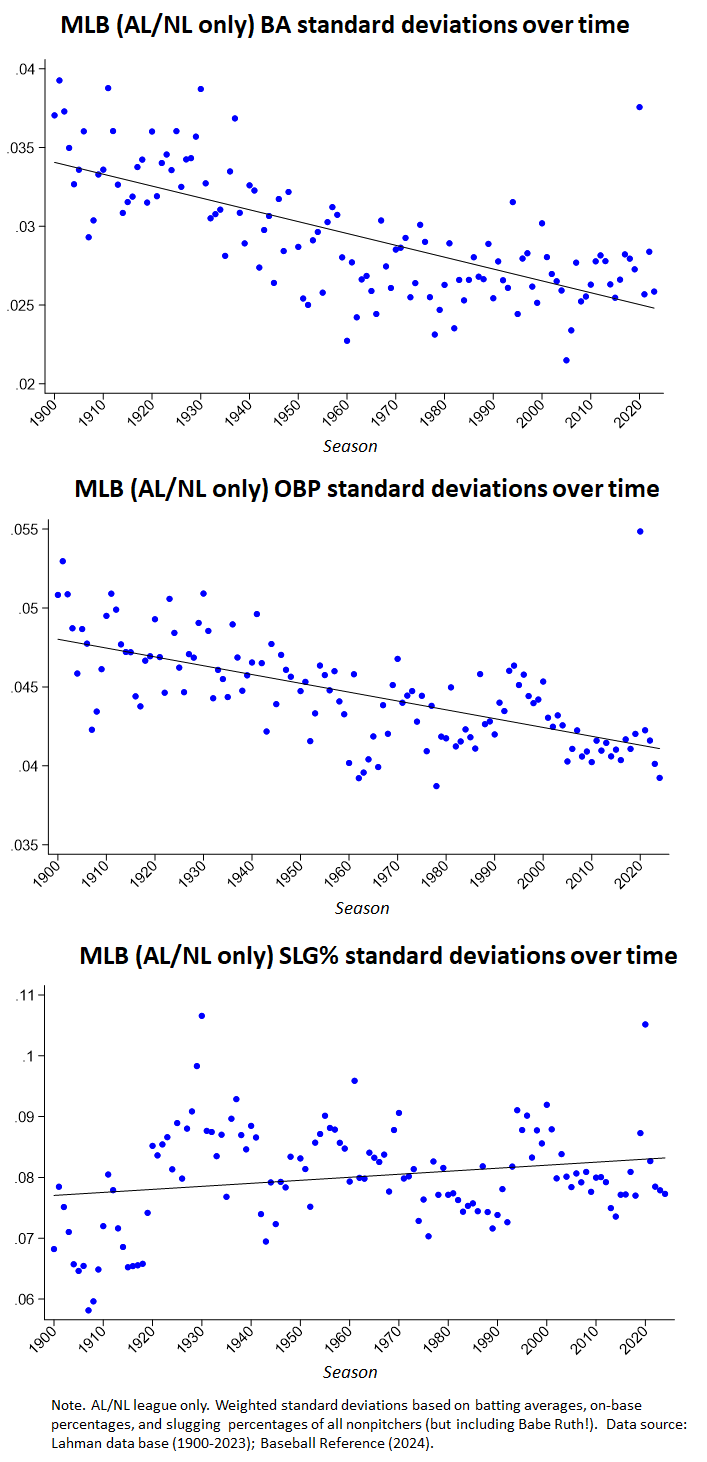
What’s weird about this, you might well be asking.
Well, the pattern—and in particular, the increase in the variability of SLG% over time—contravenes one of the most provocative and, as far as I can tell, most universally accepted conjectures about the tendencies in baseball performance and in a variety of other athletic endeavors.
The conjecture was set forth by the brilliant evolutionary biologist Stephen Jay Gould. He was addressing the extinction of the .400 hitter in baseball. He observed that the while the mean batting average, despite erratic short- to medium-term fluctuations, had remained stable over time, the standard deviation of individual averages had steadily declined.
Gould likened this pattern to one seen in the evolution of biological organisms, which gravitate toward greater uniformity in various fitness-related characteristics. Basically members of a species start to converge toward the most desirable obtainable state (along many dimensions at least) as selection forces work themselves out.
So Gould’s conjecture was that, as baseball players were evolving toward a point of maximum obtainable skill in pitching and hitting, batting performances were being squeezed closer and closer to the mean.
A .400 hitter is someone whose performance is located toward the extreme, positive end of the skill distribution. If the elite baseball-player population is tending toward its maximum obtainable state, the distribution of performances will become more dense at the mean, and the tails of the distribution fatter or less elongated. That’s what smaller SDs mean. Accordingly, as the talent pool predictably becomes deeper and deeper, it becomes less and less likely we’ll ever again see a performance that outsrips the mean by enough standard deviations to hit .400.
By the way, Gould’s insight is connected to the idea of using standardization, rather than raw numbers, to try to create the sort of commensurability in performance that allows batting averages to be compared over time. True, as the SD becomes smaller, it becomes harder and harder to dominate the field enough to bat .400. But it’s still perfectly realistic for someone to outrun the competition by the number of SDs that it took to hit .400 when BAs were more variable. It’s just that he’d now be batting well below .400! So if we want to figure out if a hitter today is as dominant as Nap Lajoie or Ty Cobb was, we should compare their z-scores—the number of SDs by which their BAs exceed the mean—rather than their raw averages.
So anyway, now maybe you are starting to see what’s weird here? On-base percentage fits the same pattern as BAs: declining variability in performance.
But SLG% does not. The SD has actually been getting bigger…. Why?!
Well, I can think of a couple of possible explanations.
One is that Gould’s conjecture is simply wrong.
That’s a possibility, but I wouldn’t bet on it (not yet, anyway). Gould was really smart, after all. Sure, smart people get it wrong—all the time; we tend to learn a tremendous amount from their errors in particular. But because they aren’t wrong all that often, it makes sense to think that the answer here is likely something else. We’re more likely to figure out if a smart conjecture is false, too, if we pit it against other hypotheses when we encounter seeming anomalies.
A more plausible alternative hypothesis, I think, is that something has changed. The game of baseball is actually evolving, and performance characteristics that were once selected on for team success are now being supplanted by others.
It seems pretty clear, after all, that batting average isn’t as tied to success as it once was—and that the game is now being transformed into one in which power pitching, as reflected in high strikeout rates, is battling with power hitting, as reflected in the spiraling rate of home runs.
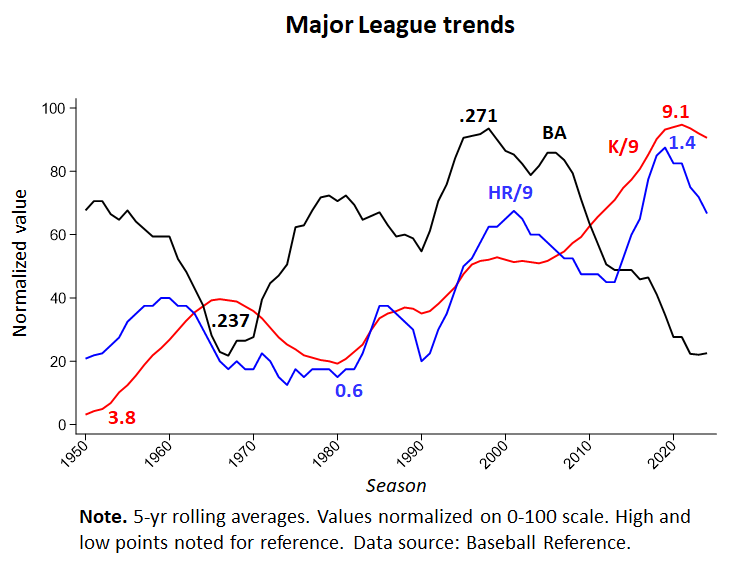If the game is now in a period of evolutionary transition, then we likely haven’t yet reached the equilibrium point yet at which variability starts to dissipate in the manner Gould surmised.
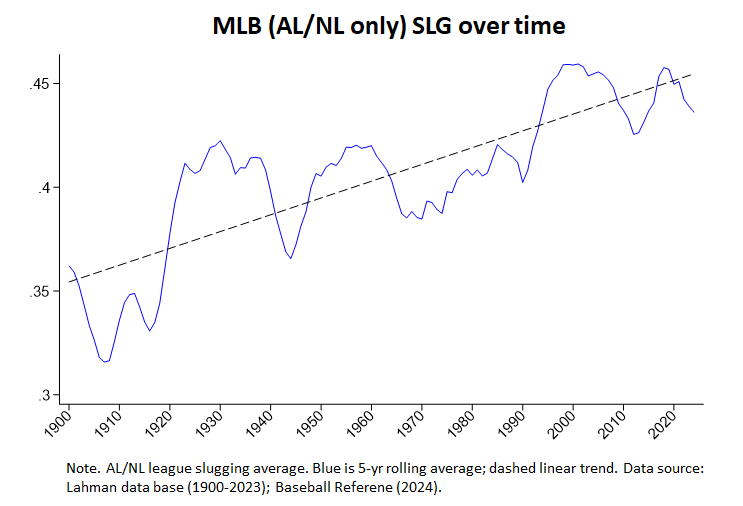
Here’s a piece of evidence that I think tends to support that: slugging percentage is a metric of performance that is increasing over time.
OBP is pretty much in stasis.
Gould thought BAs were, too, although I think we can probably conclude at this point that they are in decline; the dip over the last several decades feels more like a shift in the mean than just another of the periodic swings likely to be balanced out in the future by another glut of high-average hitting. Declining BAs are part and parcel of the apparent power-vs-power transformation that the game is undergoing.
Increasing SLG% is consistent with that. And if that’s what’s going on, then Gould isn’t wrong—the convergence toward a new mean of power just hasn’t yet taken hold to a deep enough extent for variability to start to trend downward.
Shifts in mean don’t by themselves have any implications for SDs. But if the process that generates the mean signifies a change in the system that produces it, then there could be a shift in SDs, too, until selection forces kick in and force convergence once more.
Or in any case, we now have a Gouldian prediction—that within some reasonable period, SDs will start to flatten out and decline—that can help us test whether his conjecture is right or wrong. (But we should be careful to specify a reasonable time limit; “just wait” is one of the signature dodges of pseudoscience.)
But here is one factoid that I think makes me less confident in the “evolving game” explanation:
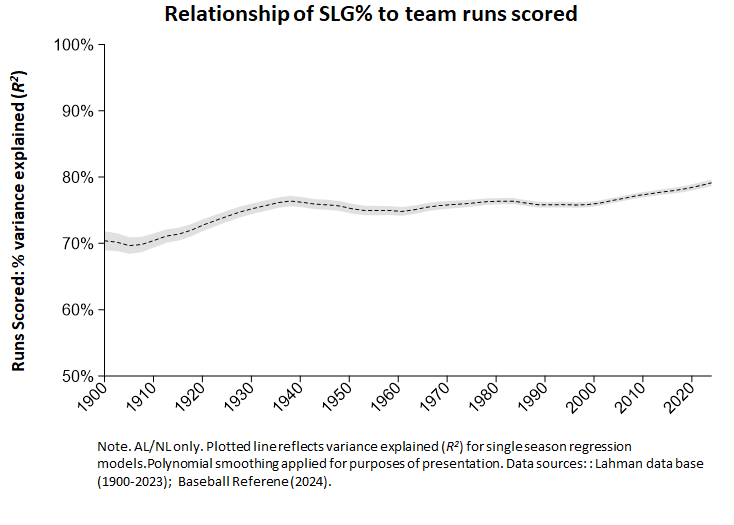
SLG%’s relationship to runs-scored has changed hardly at all since the beginning of baseball history! If a dramatic shift in the game had only recently provoked selection on the sort of skill that SLG% reflects, shouldn’t SLG% have mattered less before? If it has always mattered as much as it does now, why weren’t selection forces long driving players toward convergence toward the best obtainable state of the characteristics that produce it, in the way that Gould thought was happening with the skill reflected in BAs?
So I just dunno!
Maybe one of you do and can enlighten me about what’s going on here.
But for now, I’m just tossing this one on the “weird stuff to be investigated” pile. I’m actually really glad when I discern another phenomenon I can’t explain. The accumulation of them is an insurance policy against boredom.
And in my view, being bored is even worse than being dead.
